To nie będzie typowa recenzja. Nie, to w ogóle nie będzie recenzja. To będzie moja cegiełka w reformowaniu edukacji matematycznej w naszym kraju ;)

Niedawno pisałam o tym, że jest szereg pomocy, które standardowo są wykorzystywane na lekcjach matematyki w anglojęzycznych szkołach. Błagam, wprowadźcie je u nas! Nie skazujmy dzieci na papier - no chyba, że chcecie uczyć dzieci matematyki przez origami - na to się zgodzę.

Dobrze wiecie, że co mogę, to wyjaśniam na konkretach. Dlatego biorę na warsztat Pattern Blocks, kształty opracowane w latach  60 ubiegłego wieku przez amerykańską organizację Education Development Center. Za naszymi granicami są równie rozpoznawalne, co liczmany u nas.

Tak się fantastycznie składa, że te klocki są produkowane również w Polsce, przez krakowskie wydawnictwo Epideixis, pod nazwą Mozaika XXL.

Uczulam Was w tym miejscu, że wszystko w tych klockach jest wyraźnie wyspecyfikowane. Od kształtów, przez kolory, po grubość i średnicę. Nie ma bata, to musi być: żółty sześciokąt, beżowy  romb, niebieski romb, zielony trójkąt, czerwony trapez, pomarańczowy  kwadrat.

Zaraz wyjaśnię, dlaczego jest to sprawa życia i śmierci, ale najpierw pokażę moją wpadkę - parę lat temu, mając w pamięci mglisty obraz tego, czego używałam w angielskiej szkole, kupiłam to co widzicie na zdjęciu po prawej - 70 sztuk łudząco podobnych klocków.

Szybko okazało się, że po pierwsze, nie mam do nich kart pracy, o które natychmiast zaczęła się dopraszać moja córka, to w dodatku 70 sztuk to bzdet. Naprawdę, to jest głęboko logiczne, że Pattern Blocks są sprzedawane w paczkach po 250 sztuk (i tak jest w Mozaice XXL).

Trąbię i trąbię o tym, że mozaiki muszą spełniać specyfikację, to wypadałoby się z tego wytłumaczyć.

Co z tego, że mozaika jest zgodna ze specyfikacją?

Istotą mozaiki jest możliwość wykazania zależności budowania większych kształtów z mniejszych, na zasadzie ułamków. Więc, w sytuacji jak na zdjęciu powyżej, brak trapezu uniemożliwia rozbicie całości (sześciokąta) na dwie 1/2.

Co więc zyskujemy? Zyskujemy coś, z czym możemy pracować bez wywarzania otwartych drzwi, czyli całą otoczkę, którą już ktoś kiedyś za nas przygotował:

Narzędzia online do tworzenia własnych kart pracy [edytowalny plik Google Drawings] [generator wzorów online]

Tysiące darmowych kart pracy do pobrania z sieci

Ok, to już ustaliliśmy sobie, że to muszą być TAKIE klocki i że można sobie pobrać do nich dużo kart pracy do układania ich w kolorowe wzorki. Tylko, że nie o wzorki się tu rozchodzi. Te obrazki to dopiero czubek góry lodowej, bo sporą część podstawy programowej od przedszkola do późnych klas podstawówki można zrealizować na mozaice.

Poniżej zamieszczam skromną (słowo honoru, skromną) garść inspiracji.

Mozaika dla berbeci

Zadania typu sortowanie kształtów będą odpowiednie już dla maluchów. Z maluchami możemy również używać klocków jako liczmanów. To takie dwa pomysły, dla tych, co twierdzą, że ich dziecko może być za małe (jedna uwaga - trójkąty są małe, więc uwaga na próby degustacji).

Układanie według wzoru

Tu mogłabym napisać oddzielny artykuł, ponieważ w tym zastosowaniu pięknie możemy wprowadzić w życie dwie z montessoriańskich zasad pracy z pomocami (stopniowanie trudności oraz wbudowana kontrola błędu).

Popatrzcie tylko - stopniowanie w praktyce. Pierwszy scenariusz - układanie na kolorowej karcie ze wzorem (ta konkretna to gruba tekturowa karta, jedna z 20 dołączonych do Mozaiki XXL).

Scenariusz drugi - odwrotna strona karty i układanie na szablonie czarno-białym.

Scenariusz trzeci, znów o oczko wyżej - układanie kolorowego wzoru pod kartą pracy. W kolejnym kroku dziecko tę samą pracę wykona korzystając z czarno-białej wersji karty.

Scenariusz piąty - odrysowałam kontur tej samej lamy na papierze i teraz można ją wypełnić na wiele sposobów. W kolejnych scenariuszach możemy narzucić, że kontur ma być wypełniony konkretną liczbą kształtów. Alternatywnie możemy danemu kształtowi przypisać wartość liczbową i w trakcie układania podliczać sumę "zdobytych punktów".

Na czym polega kontrola błędu w tych zadaniach? Na tym, że kształty muszą się wpasować w kontur - w razie błędu układanka albo nie będzie zgodna z kartą pracy, albo wyjdzie poza obrys.

Rytmy

Układanie rytmów jest kolejnym zadaniem, w którym możemy stopniować trudność. Kluczowe jest to, by mieć świadomość, że rytm musi być naprawdę długi, by dziecko było w stanie dostrzec powtarzalność.

Poniżej wariant prostszy - kontynuowanie rytmu rozpoczętego. Rytm składa się z dwóch elementów i do wyboru mamy zestaw elementów, z których mamy wybrać jeden do uzupełnienia wzoru.

Wariant trudniejszy - dopasowanie elementu w środku rytmu o okresie 4.

Ciągi

Wjeżdżają pojęcia matematyczne, robi się gorąco, ale spokojnie, czterolatek to ogarnie, więc wy również.

Tym razem kształty w wydaniu 3D i historia o choince. Choinka rośnie sobie co roku o kilka elementów (ile?). Tu możemy sobie podejrzeć choinkę przez pierwsze trzy lata jej życia (rok pierwszy, rok drugi, rok trzeci).

Pytanie: Jak choinka będzie wyglądać w wieku pięciu lat? (wariant prostszy - jak choinka będzie wyglądać po kolejnym roku i po jeszcze jednym? - doprowadzi nas do tej samej odpowiedzi)

Symetria osiowa

Zadanie, które zazwyczaj podoba się dzieciom - prosimy o uzupełnienie wzoru tak, by uzyskać symetryczną strukturę.

Możemy też odwrócić sytuację i poprosić o naprawienie układu "z błędem".

Ostatnie zadanie unaocznia dziecku równoważność sumy kształtów (dwa trapezy = jeden sześciokąt).

Możemy też zabawić się w poszukiwanie osi symetrii, bo przecież tych osi może być wiele. Ja w tym celu użyłam patyczków do szaszłyków. Każdy z patyczków to jedna oś symetrii.

Bardzo łatwo możemy sprawdzić, czy prawidłowo zidentyfikowaliśmy osie symetrii - wystarczy przyłożyć lusterko narożne i zobaczyć czy odbicie fragmentu daje nam obraz całego kształtu.

Symetria obrotowa

Nie zapominajmy o symetrii obrotowej. Nawet małe dzieci będą w stanie uzupełnić obrazek tak, by wydawał się "kompletny". Wystarczy powiedzieć, że należy ułożyć kwiatki do końca, a następnie możemy porozmawiać o tym, że obracając kwiatek cały czas widzimy ten sam kształt.

Parkietaże

Ciekawe zadanie, które najprościej wykonać z dwóch kształtów podstawowych. Starsze dzieci mogą spróbować teselacji z trzech lub więcej rodzajów kształtów. Przy okazji możemy porozmawiać sobie o tym jak kolorowane są mapy polityczne i ile minimalnie kolorów do tego celu potrzeba.

A czy na zdjęciu poniżej mamy do czynienia z teselacją?

Starsi uczniowie powinni być w stanie rozpisać parkietaż jako sumę operacji - rotacji, przesunięcia, odbicia (możemy też dodać symetrię z poślizgiem).

Wypełnienia figur przystających

Możemy spróbować swoich sił w wymyślaniu różnorodnych wersji tego samego kształtu złożonego - poniżej przykłady "bombek".

Chcąc podnieść poziom trudności tego zadania możemy przygotować kostkę do gry, której każda z sześciu ścian będzie odpowiadała jednemu z kształtów podstawowych (wystarczy, że każda ze ścian będzie miała inny kolor). Tocząc kostkę możemy losować kształt, którego powinniśmy użyć.

Obliczanie obwodów

Wobraźmy sobie pomarańczowy stół - pytanie ile gości (zielone trójkąty) może przy nim usiąść? Co się dzieje kiedy wydłużamy stół?

Kształty i kąty

Zobaczcie tylko jak łatwo zilustrujemy kształtami ideę kątów naprzemianległych i wierzchołkowych. W roli głównej mozaika i patyczki do szaszłyków.

Układając dalej mozaikę i patyczki możemy sobie ładnie zilustrować twierdzenie o kątach naprzemianległych i odpowiadających. Jest to przyjemna mnemotechnika, którą dzieci mogą wykorzystać nawet na sprawdzianie z matematyki.

Kształty możemy wykorzystać do obliczeń kątów figur.

Kąty ostre i rozwarte, obliczenia miar kątów

Jak określić czy kąt jest ostry czy rozwarty? Wystarczy zapamiętać, że lusterko narożne nie może otworzyć się bardziej niż pod kątem prostym, gdy wsuwamy w nie badany kształt (kąt).

A jak obliczyć miarę kąta? Możemy na przykład ułożyć gwiazdkę i podzielić 360 przez liczbę powtórzeń figury, która zmieściła się nam w kącie pełnym.

Odwzorowanie obrazu z lustra

Znów korzystamy z lusterka narożnego. Układamy wzór pomiędzy ramionami tworzonymi przez płaszczyzny lustra. Następnie prosimy dziecko by samodzielnie ułożyło cały wzór, który może podejrzeć w lusterku.

Działania na ułamkach

Zobaczcie tylko jak łatwo wykonywać działania na ułamkach - na zdjęciu w pierwszym rzędzie mamy jedność, dwie  1/2, trzy 1/3 oraz sześć 1/6

W drugim rzędzie mamy natomiast efekt sumowania 1/2 i 1/3. Nie uważacie, że nawet bez obliczeń suma ta ewidentnie wygląda na 5/6?

O ile chcielibyście zmienić podstawę obliczeń, to możemy się umówić inaczej - jedność to dwa sześciokąty, jak poniżej.

Przy takiej umowie zyskujemy do obliczeń następujące ułamki - 1/2, 1/4, 1/6 i 1/12.

Zadanie dla Was (na zdjęciu): ile to jest 2/4 dodać 5/6?

Zwróćcie uwagę, że ułamki niewłaściwe również bardzo elegancko będą dawały się reprezentować przy pomocy kształtów. Sprowadzanie do wspólnego mianownika podobnie - czysta poezja!

Skalowanie i pola powierzchni

Zadanie dość ambitne - przeskalować dany kształt o czynnik X (na zdjęciu skalowanie ze skalą 2). Co się wtedy dzieje z polem powierzchni?

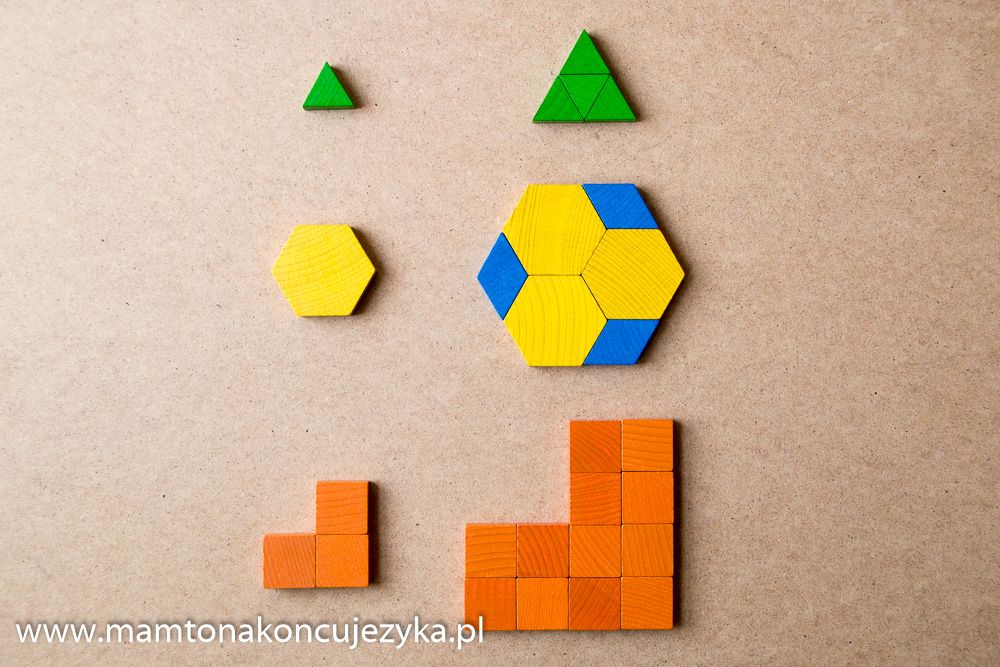
Mozaika i rozwijanie zdolności językowych

Bardzo przyjemne zadanie dla dwóch osób. Jedna buduje wzór w ukryciu, po czym instruuje drugiego gracza jak ma odwzorować układ. Ubaw murowany, ponieważ precyzja opisów u dzieci zazwyczaj nie jest wysoka.

Podsumowanie

Ciężko było mi pisać ten artykuł, bo cały czas miałam z tyłu głowy, jak bardzo chciałabym, żeby coś się ruszyło w naszym systemie edukacji i że są gotowe fantastyczne narzędzia, które kompletnie olewamy.

Pattern Blocks (Mozaika) idealnie się do tego nadają.

I celowo nie pisałam dyrdymałów typu "pudełko jest ciężkie, duże, klocki pięknie wykonane, drewniane, a karty trwałe". Oczywiście jest to prawdą, ale to nic nie wnosi. Ważny jest potencjał i różnorodność zastosowań, do których można wykorzystać daną pomoc. A to, mam nadzieję, udało mi się pokazać.

Mozaikę XXL kupicie na stronie wydawnictwa Epideixis

Dziękuję ogromnie Wydawnictwu Epideixis, że zgodziło się zostać partnerem mojego mini-cyklu matematycznego inspirowanego dydaktyką matematyki w krajach anglosaskich.

Książki, które polecam, rekomenduję Wam z całego serca. Jeśli zechcesz dokonać zakupu przez któryś z linków przeze mnie zamieszczonych, dostanę z tego tytułu małą prowizję. Nie ma to wpływu na cenę książki, a będzie to formą wyrażnia wdzięczności za moją pracę.

Podoba Ci się to co robię? Chcesz być na bieżąco? Jeśli zainteresował Cię ten artykuł, to zapraszam do polubienia mojej strony na Facebooku